10/04/2005
Retour éternel
« Hier n’est pas un jalon que nous aurions dépassé, c’est un caillou des vieux sentiers rebattus des années qui fait partie de nous irrémédiablement, que nous portons en nous, lourd et menaçant. » (Beckett)

A partir de son arrivée aux États-Unis en 1940, Gödel délaisse la théorie des ensembles pour étudier la relativité. A Princeton, il prend l'habitude de longues promenades avec Einstein durant lesquelles ils conversent au sujet des implications philosophiques de leurs travaux. C'est ainsi que Gödel en vient à concevoir que le voyage dans le temps est possible dans le cadre des équations de la relativité générale d'Einstein : « En faisant en fusée un voyage circulaire dont la courbure est suffisamment grande, il est possible, dans ces mondes, d'atteindre n'importe quelle région du passé, du présent et du futur et de revenir, exactement comme il est possible dans d'autres mondes d'atteindre des points distants dans l'espace. » (A remark about relationship between relativity and idealistic philosophy*, 1949)
Si la matière est adéquatement disposée dans l'espace-temps, alors peut se produire une courbe fermée de genre temps. Celle-ci peut concerner soit une partie soit la totalité de l'univers. Bien plus, il est concevable que chacun des points de l'univers comprenne des boucles temporelles. D'abord calculées dans un espace statique, ces courbes fermées de genre temps seront généralisées par Gödel à un espace en expansion.
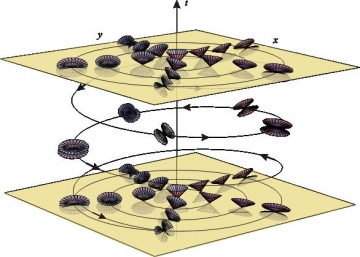
A priori, la théorie de la relativité semble interdire de telles trajectoires fermées. En effet, la trajectoire d'un point est restreinte par un cône de lumière dont il constitue le sommet. Puisque la vitesse maximale de l'information est celle de la lumière, l'ensemble des événements avec lesquels il peut communiquer est limité au volume intérieur du cône. Néanmoins, chaque point situé dans le cône est lui-même le sommet d'un autre cône de même caractéristique angulaire mais qui peut être incliné par rapport au premier par la médiation d'une force adéquate. D'inclinaison en inclinaison, rien n'empêche de faire l'hypothèse d'une trajectoire revenant finalement à son point de départ. La trajectoire en question se déroulant dans l'espace-temps, l'hypothétique mobile se retrouve donc non seulement à son point de départ spatial mais aussi temporel. C'est bien d'un voyage dans le passé dont il s'agit.
Cette démonstration de Gödel sera validée par Einstein. Certes, et Gödel le reconnaît bien volontiers, l'existence de telles courbes fermées n'est pas avérée, elle est seulement possible. Tout dépend en fait de la répartition effective de la matière dans l'univers.
Alors, le temps existe-t-il vraiment ? Revenir dans le passé implique que le passé est présent donc qu'il n'est pas passé. Si le passé est présent, le temps n'existe pas. Dans ce cadre théorique, le temps est tout au plus un phénomène dérivé puisque des configurations matérielles qui l'excluent sont concevables.
On connaît les paradoxes classiques des voyages dans le temps. Par exemple, si un tel voyageur tuait l'un de ses ancêtres, il ne pourrait pas naître et donc le tuer. S'il ne peut pas le tuer, il pourra naître et donc il sera à même d'effectuer ledit voyage et, derechef, de le tuer. Ad libitum. En règle générale, changer le passé revient à modifier le présent dont l'on est censé partir au risque de rendre le départ dans le passé impossible puisqu'on annihile le présent corrélatif.
Dans le cas évoqué par Gödel, le voyageur qui commence son voyage serait en fait indiscernable du voyageur qui l'achève. Deux cas sont envisageables. Ou bien : au début de son périple, il a le souvenir de son futur et vit sa trajectoire dans l'espace-temps comme un déjà vu. Ou bien : la fin du voyage, c'est-à-dire son début, est une mort au moins psychique puisque le souvenir du parcours est aboli, la perte de sa mémoire est aussi celle de son identité.
En tous cas, à l'instant même où le cercle se ferme, rien ne distingue, physiquement ou psychiquement, le voyageur de son double hypothétique et éternel.
« "Est-il sûr que je veuille le faire un nombre infini de fois ?", ce sera pour toi le centre de gravité le plus solide. » (Nietzsche)
*Add. du 12/10/2010:
Notre traduction de cet article, ici.
20:05 | Lien permanent | Commentaires (0)




Les commentaires sont fermés.